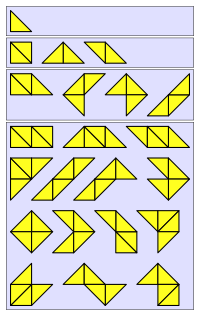
In recreational mathematics, a polyabolo (also known as a polytan) is a polyform with an isosceles right triangle as the base form.[1]
The name is a back formation from 'diabolo' although the shape formed by joining two triangles at just one vertex is not a proper polyabolo. On a false analogy as if di- in diabolo means twice, polyaboloes with from 1 to 10 triangles are called respectively monoboloes, diaboloes, triaboloes, tetraboloes, pentaboloes, hexaboloes, heptaboloes, octaboloes, enneaboloes, and decaboloes.
There are two ways in which a square in a polyabolo can consist of two isosceles right triangles, but polyaboloes are considered equivalent if they have the same boundaries. The number of nonequivalent polyaboloes composed of 1, 2, 3, … triangles is 1, 3, 4, 14, 30, 107, 318, 1116, 3743, … (sequence A006074 in OEIS).
Polyaboloes that are confined strictly to the plane and cannot be turned over may be termed one-sided. There are now four diaboloes (instead of three), six triaboloes (instead of four), 22 tetraboloes (instead of 14), and so on.
A non-simply connected polyabolo is one that has one or more holes in it. The smallest value of n for which an n-abolo is non-simply connected is 7.
Tiling rectangles with copies of a single polyabolo[]
In 1968, David A. Klarner defined the order of a polyomino. Similarly, the order of a polyabolo P can be defined as the minimum number of congruent copies of P that can be assembled (allowing translation, rotation, and reflection) to form a rectangle.
A polyabolo has order 1 if and only if it is itself a rectangle. Polyaboloes of order 2 are also easily recognisable. Solomon W. Golomb found polyaboloes, including a triabolo, of order 8.[2] Michael Reid found a heptabolo of order 6.[3]
References[]
- ↑ Gardner, Martin (June 1967). "The polyhex and the polyabolo, polygonal jigsaw puzzle pieces". Scientific American 216 (6): 124–132.
- ↑ Golomb, Solomon W. (1994). Polyominoes (2nd ed.). Princeton University Press. pp. 101-101. ISBN 0-691-02444-8.
- ↑ Goodman, Jacob E.; O'Rourke, Joseph (2004). Handbook of Discrete and Computational Geometry (2nd ed.). Chapman & Hall/CRC. pp. 349-349. ISBN 1-58488-301-4.
External links[]
- Weisstein, Eric W., "Polyabolo" from MathWorld.
This geometry-related article contains minimal information concerning its topic. You can help the Mathematics Wikia by adding to it.