| Regular hendecagon | |
|---|---|

| |
| Edges and vertices | 11 |
| Schläfli symbols | {11} |
| Coxeter–Dynkin diagrams | |
| Symmetry group | Dihedral (D11) |
| Area (with = edge length) |
|
| Internal angle (degrees) |
180°×(1-2/11) =147°.27 |
In geometry, a hendecagon (also undecagon[1]) is an 11-sided polygon. The name "undecagon" is often seen as incorrect, but the matter is up for debate. The Greek prefix 'hen', is preferable to the Latin 'uni' or 'un'.[2] A regular hendecagon has internal angles of 147.27 degrees. The area of a regular hendecagon with side length is given by
A regular hendecagon is not constructible with compass and straightedge.
Use in coinage[]
The Canadian dollar coin, the loonie, is patterned on a regular hendecagonal prism, as is the Indian two-rupee coin.
It was also patterned on the Susan B. Anthony dollar of the United States from 1979-1981 and again in 1999.
See also[]
References[]
Related shapes[]
The hendecagon shares the same set of 11 vertices with four regular hendecagrams, {11/2}, {11/3}, {11/4}, {11/5}.
Petrie polygons[]
The regular hendecagon is the Petrie polygon for 10-dimensional uniform polytopes of the simplex family, projected in a skew orthogonal projection.[1][2]
 10-simplex |
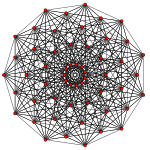 Rectified 10-simplex |
 Birectified 10-simplex |
 Trirectified 10-simplex |
 Quadrirectified 10-simplex |
External links[]
- Properties of an Undecagon (hendecagon) With interactive animation
- Weisstein, Eric W., "Hendecagon" from MathWorld.
| ||||||||||||||||||||
ar:أحادي عشري ast:Endecágonu cs:Jedenáctiúhelník eo:Dekunulatero gl:Endecágono it:Endecagono hu:Tizenegyszög nl:Elfhoek no:Hendekagon nn:Hendekagon pt:Hendecágono sr:Једанаестоугао th:รูปสิบเอ็ดเหลี่ยม
- ↑ Coxeter, H. S. M. Petrie Polygons. Regular Polytopes, 3rd ed. New York: Dover, 1973. (sec 2.6 Petrie Polygons pp. 24–25)
- ↑ Humphreys, James E. (1992), Reflection Groups and Coxeter Groups, Cambridge University Press, pp. 80 (Section 3.16, Coxeter Elements, table 2, Coxeter number for An is n+1), ISBN 978-0-521-43613-7, http://books.google.com/?id=ODfjmOeNLMUC



