
The truncated tetrahedron with hexagons replaced by triangles is not a convex deltahedron because it is not strictly convex.
A deltahedron (plural deltahedra) is a polyhedron whose faces are all equilateral triangles. The name is taken from the Greek majuscule delta (Δ), which has the shape of an equilateral triangle. There are infinitely many deltahedra, but of these only eight are convex, having 4, 6, 8, 10, 12, 14, 16 and 20 faces. The number of faces, edges, and vertices is listed below for each of the eight convex deltahedra.
The deltahedra should not be confused with the deltohedra (spelled with an "o"), polyhedra whose faces are geometric kites.
The eight convex deltahedra[]
| Name | Image | Faces | Edges | Vertices | Vertex configurations | Symmetry group |
|---|---|---|---|---|---|---|
| regular tetrahedron |  |
4 | 6 | 4 | 4 × 33 | |
| triangular dipyramid |  |
6 | 9 | 5 | 2 × 33 3 × 34 |
|
| regular octahedron |  |
8 | 12 | 6 | 6 × 34 | |
| pentagonal dipyramid | 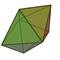 |
10 | 15 | 7 | 5 × 34 2 × 35 |
|
| snub disphenoid |  |
12 | 18 | 8 | 4 × 34 4 × 35 |
|
| triaugmented triangular prism |  |
14 | 21 | 9 | 3 × 34 6 × 35 |
|
| gyroelongated square dipyramid |  |
16 | 24 | 10 | 2 × 34 8 × 35 |
|
| regular icosahedron |  |
20 | 30 | 12 | 12 × 35 |
Three of the deltahedra are Platonic solids (polyhedra in which a constant number of identical regular faces meet at each vertex). These are:
- the 4-faced deltahedron (or tetrahedron), in which three faces meet at each vertex
- the 8-faced deltahedron (or octahedron), in which four faces meet at each vertex
- the 20-faced deltahedron (or icosahedron), in which five faces meet at each vertex
In the 6-faced deltahedron, some vertices have degree 3 and some degree 4. In the 10-, 12-, 14-, and 16-faced deltahedra, some vertices have degree 4 and some degree 5. These five irregular deltahedra belong to the class of Johnson solids: convex polyhedra with regular polygons for faces.
Deltahedra retain their shape, even if the edges are free to rotate around their vertices so that the angles between edges are fluid. Not all polyhedra have this property: for example, if you relax some of the angles of a cube, the cube can be deformed into a non-right square prism.
Non-convex forms[]
There are an infinite number of nonconvex forms.
Some examples of non-convex deltahedra:
- Great icosahedron - a Kepler-Poinsot solid.
Others can be generated by adding equilateral pyramids to the faces of all 5 regular polyhedra:
- Equilateral triakis tetrahedron
- Equilateral tetrakis hexahedron
- Equilateral triakis octahedron (stella octangula)
- Equilateral pentakis dodecahedron
- Equilateral triakis icosahedron
Also by adding inverted pyramids to faces:
- Wenninger's third stellated icosahedra
 Great icosahedron (20 intersecting triangles) |
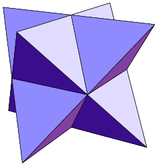 stella octangula (24 triangles) |
 Third stellation of icosahedron (60 triangles) |
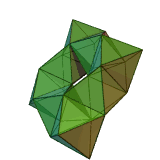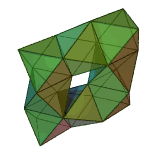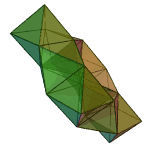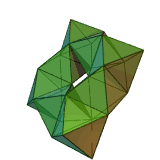 A toroidal deltahedron (48 triangles) |
External links[]
References[]
- Freudenthal, H. and van der Waerden, B. L. "Over een bewering van Euclides". ("On an Assertion of Euclid") Simon Stevin 25, 115—128, 1947. (They showed that there are just 8 convex deltahedra. )
- H. Martyn Cundy Deltahedra. Math. Gaz. 36, 263-266, Dec 1952. [2]
- H. Martyn Cundy and A. Rollett Deltahedra. §3.11 in Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., pp. 142–144, 1989.
- Charles W. Trigg An Infinite Class of Deltahedra, Mathematics Magazine, Vol. 51, No. 1 (Jan., 1978), pp. 55–57 [3]
- M. Gardner Fractal Music, Hypercards, and More: Mathematical Recreations, Scientific American Magazine. New York: W. H. Freeman, pp. 40, 53, and 58-60, 1992.
- A. Pugh Polyhedra: A Visual Approach. Berkeley, CA: University of California Press, pp. 35–36, 1976.
eo:Egallatera trianguledra pluredro it:Deltaedro nl:Deltaëder pt:Deltaedro sk:Deltaéder th:เดลตาฮีดรอน






